通常の媒質は誘電率と透磁率はともに正の値をとります。このため媒質中を伝播する電磁波 の位相速度と群速度は同一の符号をとることが示されます。近年議論されているメタマテリアルは電磁波波長に比べて十分小さな構造を人工的に構築することによって、誘電率と透磁率を同時に負とする媒質のことをいいます。この場合には電磁波の位相速度と群速度が互いに逆を向くことが証明されます。この性質を用いてさまざまな信号処理回路、レンズ、アンテナなどの提案が各所でなされています。
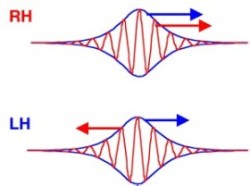
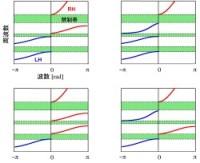
　右図では青矢線で群速度の、赤で位相速度の向きをそれぞれしめしています。RH（Right-handed、右手系）とは誘電率・透磁率が同符号である場合をいい、矢線は同一の向きをとります。一方、LH（Left-handed、左手系）とはメタマテリアルの場合をいい、互いに逆の向きをとります。通常媒質で電界、磁界に対して波動ベクトルが右ねじと同じように向くことを反映してRH系、メタマテリアルではちょうどこれが反転するためLH系などと呼称されることがあります。

　電子回路で簡単にメタマテリアルを構成する手法は右図に示すCRLH(=Composite Right-and-Left-Handed)線路を用いることです。2002年に米国、加国で提案された比較的広帯域のメタマテリアルといえます。特徴的な回路要素は図に示す４つであり、その大小によってさまざまな分散特性が発現します。

　CRLH線路は右図にしめす分散関係を満足します。横軸に電磁波波長、縦軸に周波数をとっています。前後しますが波動の空間スケールと時間スケールの間の関係を分散関係と呼びます。線形な波動は重ね合わせの原理を満足しますから、周波数に対する波数が確定していれば任意の波形の伝播特性をあらかじめ予測することができます。
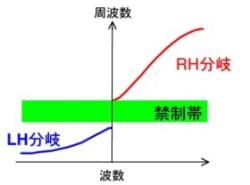
　高周波側では右手系の低周波側では左手系の属性が現れます。図にLH分岐と示している領域が後者にあたります。右手系領域と左手系領域の間には波動伝播が許されない禁制帯が存在しています。

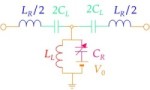
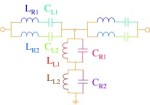
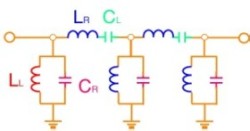
　右（上段）の回路図は右手系容量を電圧可変とすることによって波動に非線形性を導入した1次元非線形CRLH線路を示しています。もとより分散性の極めて大きなCRLH線路に非線形性を導入するといわゆる包絡ソリトンが生成することが予想されます。
　高速性・設計性に秀でたショットキ・バラクタを念頭においた解析によって系が非線形シュレディンガー方程式によって記述されることが示されます。これは光ファイバー中の波動伝播においても現れるもので、Sech関数で記述されるソリトン解を持つことが知られています。
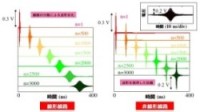
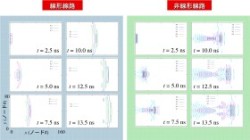
　右（下段）図には1次元非線形CRLH線路の数値解析結果の一例をしめします。左には比較のため線形CRLH線路でのパルス伝播の様子を、右に非線形CRLH線路でのそれを示しています。左の図面からは分散性によってCRLH線路上では波形は大きく変化している様子が確認できます。一方、右側の図面では波形は定常化しソリトンが生成されている様が見て取れます。包絡線はよくSech関数で表されています。

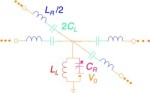
　CRLH線路には次元拡張性があります。2次元に展開した2次元CRLH線路は負の屈折率をもつ周波数においては興味深い回折・反射特性を呈します。右（上段）図に示すように右手系容量にバラクタを与えることによって得られる2次元非線形CRLH線路を考えます。すると波動伝播は2次元非線形シュレディンガー方程式で記述されることが示されます。
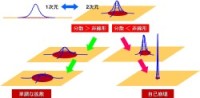
　非線形シュレディンガー方程式は1次元ではソリトン解を持ちますが、2次元ではそうはなりません。右（下段）図に示すところですが2次元では線路の分散性と非線形性は必ずいずれかの寄与が他方を凌駕することになります。分散性が非線形性に勝る場合には波形は単調に拡散して減衰していきます。一方、非線形性が分散性に勝る場合には波動自体に電磁パワーの集中する自己集束という減少によって崩壊してしまいます。実際のバラクタはしかし有限の電圧領域でのみ非線形性を呈します。この制限された非線形性であれば分散性とつりあい、波形の定常化が可能となります。

　右の図面では2次元CRLH線路上の波動伝播を数値解析した結果です。ショットキ・バラクタを考えています。順方向では容量値が一定とする近似によって非線形性を制限しています。比較のため、左に線形線路、右に非線形線路の様子です。６つの異なる時間における波形等高線を示しています。左端中心のノードから包絡パルスを入力しています。線形線路の場合には単調な拡散が見られます。非線形線路の場合をみると局在化したパルスが減衰せずに進行している様子が確認できます。このような局在波動が随意とできればマイクロ波−テラヘルツ帯電磁波をあたかもレーザー光のように扱う新しい信号処理系を構築することができるものと考えています。

　LC対が一つずつある合計二つあることがCRLH線路の特徴でした。これをおのおの二つ設けるとどういうことが起こるでしょう。興味深いことに左手系分岐、右手系分岐が合わせて四つ、禁制帯が３つ現れます。
　右（下段）図に分散の例を示しました。線路パラメータの大小によって分岐の配置を設計することができます。もっとも周波数の小さな分岐、もっとも大きな分岐はそれぞれ、左手系、右手系に確定していますが、他の二つの分岐の属性は設計が任意です。たとえば、単一の大きさの波数に対応する周波数がCRLH線路の倍の4つになります。CRLH線路をこのように拡張することで応用シーンの拡大が可能となります。

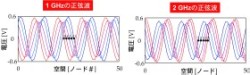
　二段CRLH線路の興味深い性質の一つは、二つの異なる周波数でその波数と特性インピーダンスを同時に一致させることができることです。波数が一致しているという性質は波長を単位としてながめると単一の線路がそれぞれの周波数で同一の距離を持つ（電気長が一致する）ことを意味します。また特性インピーダンスが一致すると任意の負荷に対して反射波振幅が同一になるという性質が生じます。基本的には二つの周波数を全く同一の回路で同様に動作させることが可能となるわけです。この性質を用いた新しいマイクロ波−ミリ波回路を検討してみることは非常に有意義といえます。

• Back To Top
• Home