半導体プラズマの物性と利用に関する研究
[1] 半導体プラズマ中の波動制御
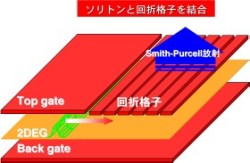
半導体プラズマ中にはさまざまな分散特性を持った波動励起が可能であることが知られています。近傍に金属電極を配した2次元電子ガス(two-dimensional electron gas, 2DEG)プラズマは一層興味の対象足りうるものです。流体的振る舞いによって電子輸送は本質的な非線形性を有しています。こうして2DEG中に電子ソリトンを励起することが可能となります。
たとえばこのソリトンと近接する回折格子を結合させることによってSmith−Purcell効果を期待することによってTHz帯電磁波を生成することが可能と考えています。Smith−Purcell効果とは高速に移動する電荷がその周囲にまとうエバネセント波の一部を回折格子を介して放射波に変換する作用のことを言います。ソリトンの速度は通常のドリフト・拡散速度に対して一桁の高速性を持つことが示され、効果的にこれを引き起こすことができるのです。
たとえばこのソリトンと近接する回折格子を結合させることによってSmith−Purcell効果を期待することによってTHz帯電磁波を生成することが可能と考えています。Smith−Purcell効果とは高速に移動する電荷がその周囲にまとうエバネセント波の一部を回折格子を介して放射波に変換する作用のことを言います。ソリトンの速度は通常のドリフト・拡散速度に対して一桁の高速性を持つことが示され、効果的にこれを引き起こすことができるのです。
[2] 二次元電子ガス中のプラズマ波動の伝播特性
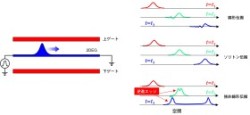
上下をゲート金属で遮蔽された2DEGでは露にソリトン方程式を導くことができます。線形分散では高周波ほど遅れる性質があり、一方非線形性はこれに対向します。電子密度の局所的な揺らぎの振幅が大となるにつれてソリトンが生成され、さらに振幅大となると拡散の効果が顕在化し逆進エッジの成長が予想されます。こうした大枠での理解を進め、新らしい素子イメージの確立に邁進しています。
[3] ENOスキームによる流体電子輸送の描写
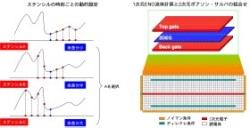
2DEGプラズマの物性を明らかにするためにEssentially Non-Oscillatory (ENO)スキームを用いた有限差分流体素子解析ツールを開発しています。電子デバイスでは桁違いの電荷密度の領域を同時にとく必要があり高精度スキームの利用が不可欠です。現況では1次元ENO計算と2次元ポアソン・サルバを組み合わせた形態で2DEG中の半導体ソリトンの物性などを検証しています。
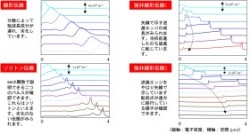
[4] 二次元電子ガス中の非線形プラズマ波動数値計算結果
ENO計算の一例を図面として提示します。ゲートで遮蔽された2DEG中の電子パルスの振る舞いをその振幅を変化させて計算した結果です。小振幅の場合には線形分散性が顕著です。振幅を増加させていくとソリトン生成や逆進パルスエッジなどが見て取れます。解析的な手法で得た帰結がうまく数値的に表現できることがわかります。実践素子設計に向けて完成度向上を進めます。